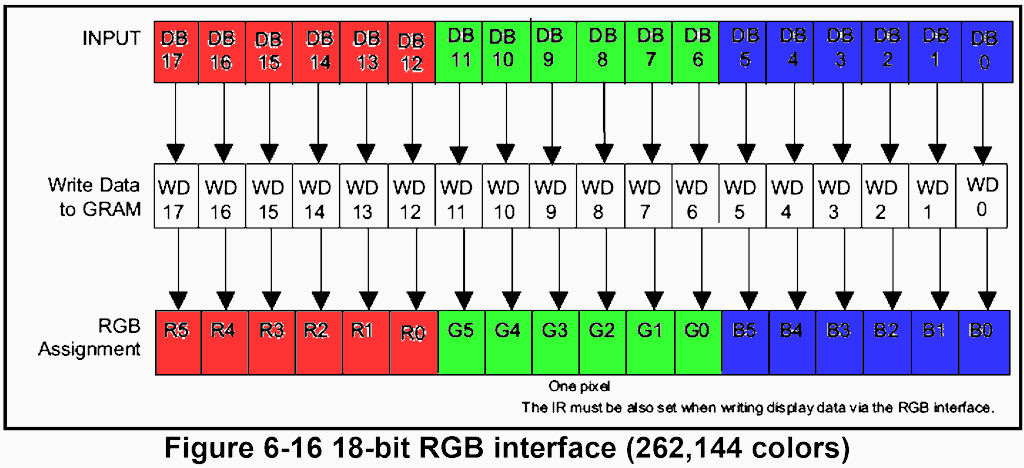
Hello All,
I’m looking at the crystalfontz CFAF240400D-030T RGB display.
https://www.crystalfontz.com/product/cfaf240400d030t-display-module-tft-lcd-240x400-graphical
The reason I’m looking at it is because of size. It is a near perfect fit for my needs. Through research I’m learning this display may not be the easiest to interface with but size is exactly what we need.
My Application:
I’m designing a prototype status indicator screen for an airplane cockpit. Input’s from multiple sources will be coming into a master control unit (MCU). In this case we are prototyping the MCU as a raspberrypi 3 Model B.
The concept is to have a PI run a script that loops through the GPIO pins listening for state changes. If a pin changes states, the LCD is to display text (colored text and background color) that indicates the current condition. Example; engine fire, low fuel, cabin pressure, door unlocked, door open and so forth. The background color behind each text string will be unique. Depending on the severity of the condition the background may be red and text yellow to indicate emergency which requires immediate attention.
This will be the first time I’m working with a TFT LCD. I’m also very green with raspberrypi’s. I’m a mechanical engineer stretching my legs with electrical engineering concepts.
Couple questions that I could use some confirmation or high level direction on.
1. Are there any known tutorials on connecting this display to a PI?
2. Are there any known recommendations for connecting components that we should consider? (example IDA connector and ribbon cable to GPIO pi header)
3. Is this LCD capable of I2C or SPI communication? Or just parallel interface?
4. Are there any known wiring diagrams or tutorials to help with setup?
5. Is there any known recommended chip, breakout board or custom cable that could consolidate the amount of wires required to drive data to and from the LCD and PI? (example serial to parallel converter)
Any high level guidance or product selection is appreciated. Thank you!
I’m looking at the crystalfontz CFAF240400D-030T RGB display.
https://www.crystalfontz.com/product/cfaf240400d030t-display-module-tft-lcd-240x400-graphical
The reason I’m looking at it is because of size. It is a near perfect fit for my needs. Through research I’m learning this display may not be the easiest to interface with but size is exactly what we need.
My Application:
I’m designing a prototype status indicator screen for an airplane cockpit. Input’s from multiple sources will be coming into a master control unit (MCU). In this case we are prototyping the MCU as a raspberrypi 3 Model B.
The concept is to have a PI run a script that loops through the GPIO pins listening for state changes. If a pin changes states, the LCD is to display text (colored text and background color) that indicates the current condition. Example; engine fire, low fuel, cabin pressure, door unlocked, door open and so forth. The background color behind each text string will be unique. Depending on the severity of the condition the background may be red and text yellow to indicate emergency which requires immediate attention.
This will be the first time I’m working with a TFT LCD. I’m also very green with raspberrypi’s. I’m a mechanical engineer stretching my legs with electrical engineering concepts.
Couple questions that I could use some confirmation or high level direction on.
1. Are there any known tutorials on connecting this display to a PI?
2. Are there any known recommendations for connecting components that we should consider? (example IDA connector and ribbon cable to GPIO pi header)
3. Is this LCD capable of I2C or SPI communication? Or just parallel interface?
4. Are there any known wiring diagrams or tutorials to help with setup?
5. Is there any known recommended chip, breakout board or custom cable that could consolidate the amount of wires required to drive data to and from the LCD and PI? (example serial to parallel converter)
Any high level guidance or product selection is appreciated. Thank you!
Looking for additional LCD resources? Check out our LCD blog for the latest developments in LCD technology.